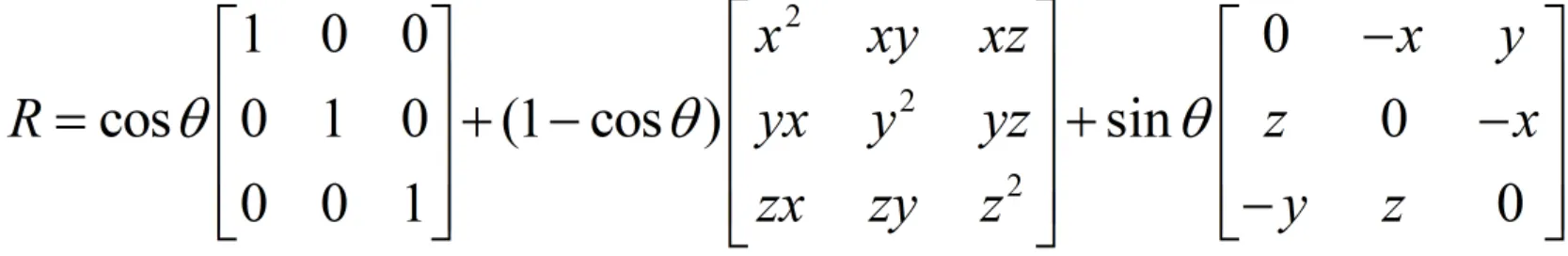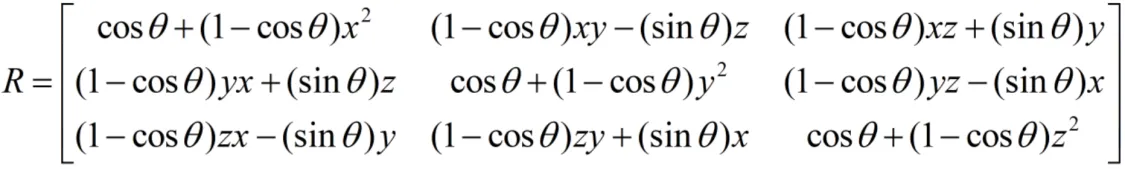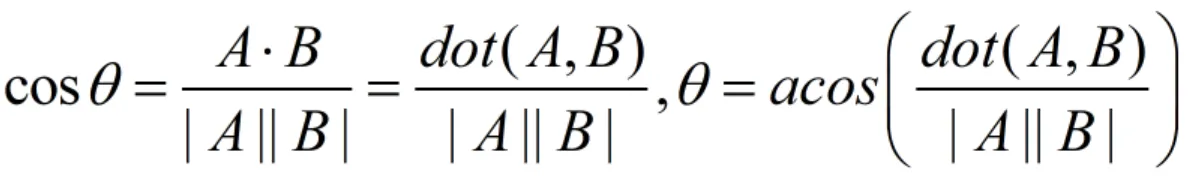需求
将空间一个矢量u旋转到v,求旋转矩阵R
方法
直观上,绕某个轴k(x,y,z)旋转角度θ即可。
其中k是单位矢量,计算方法为u×v,在 Matlab 中为cross(u,v),然后再归一化。
θ:右手大拇指指向k,其余四指环绕的方向为θ的正方向
根据罗德里格旋转公式-百度百科与旋转矩阵-维基百科,有v=Ru,其中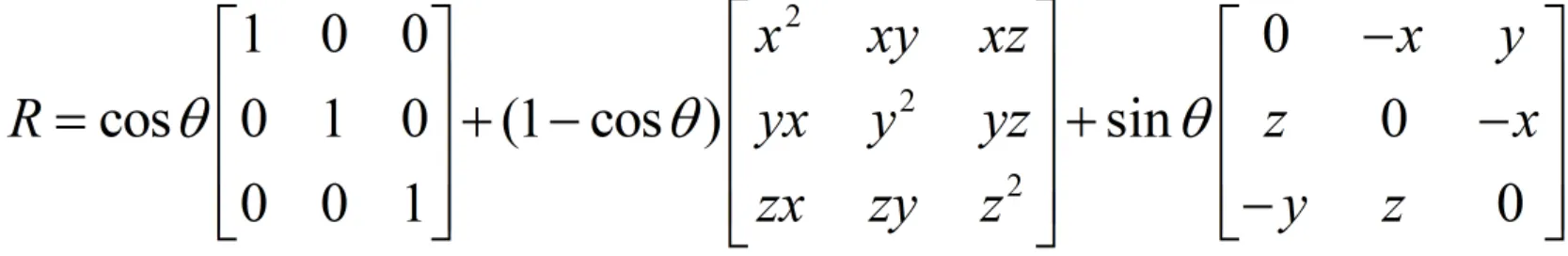
可化简为:
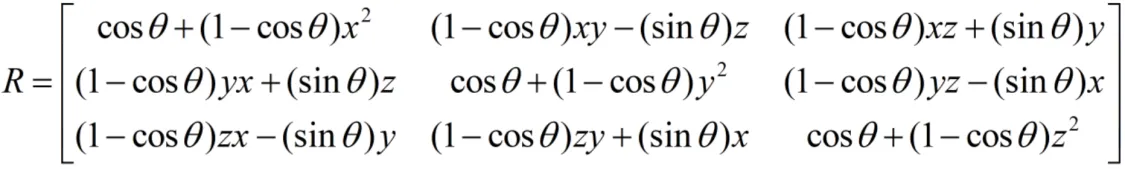
补充:角度说明

要把 B1 或者 B2 旋转到 A 的位置时,不用担心旋转角度是 180° 到 360° 之间的问题,因为之所以你认为角度会大于 180 是因为你已经假设了一个转轴。实际上,参考B<font style="color:rgb(33, 33, 33);">×A</font>定义的转轴,旋转角度始终在 0~180° 之间。
点积:计算两矢量角度大小(0~180)
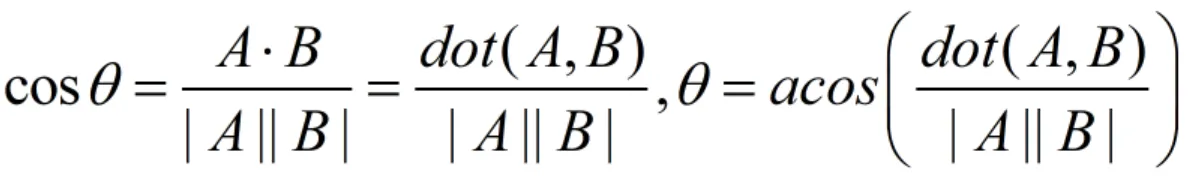
叉积:计算转轴(含方向)
在几何上,cross(A,B) =A×B ,A×B 同时与 A 和 B 正交

综上
- 计算 A->B 旋转中将用于参考的转轴
k,k=cross(A,B),再归一化
- 使用点积计算两个矢量 A 和 B 的夹角
a(0~180)
- 则
矢量A绕转轴k旋转角度a即可与矢量B重合
Matlab 代码
计算从原始向量oriVec到目标向量tarVec的旋转矩阵R
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| clc;clear
oriVec = [0; 1; 1]; % origin Vec
tarVec = [0; -1; -1]; % target Vec
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
k = cross(oriVec,tarVec);
Nk = length(find(k==0));
Nzero = length(find(tarVec==0));
if Nk==3 && Nzero==2
II = find(tarVec==0);
tarVec(II(1)) = tarVec(II(1))+1e-10;
k = cross(oriVec,tarVec);
else
[~,II] = max(abs(tarVec));
tarVec(II) = tarVec(II)+1e-10;
k = cross(oriVec,tarVec);
end
k = k/norm(k);
theta = acos(dot(oriVec,tarVec)/norm(oriVec)/norm(tarVec));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
x = k(1); y = k(2); z = k(3);
CA = cos(theta); SA = sin(theta); oneCA = 1 - CA;
R = [CA+oneCA*x*x, oneCA*x*y-SA*z, oneCA*x*z+SA*y;
oneCA*y*x+SA*z, CA+oneCA*y*y, oneCA*y*z-SA*x;
oneCA*z*x-SA*y, oneCA*z*y+SA*x, CA+oneCA*z*z];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
targetTest = R*oriVec
|
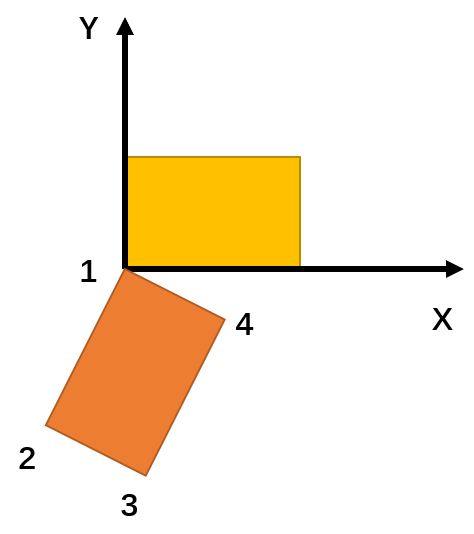
然后就可以用R去旋转空间内的任意矢量,例如下面将四边形 14 边旋转到 Y 轴,可以确定 R,然后 R 再乘以另外三个矢量即可得到旋转后的新的四边形坐标。